量子力学Ver.1~Ver.2
に書いたところ、何百人か読んでいたが誰も意味がわからなかったようなので、削除してこちらに書き直すことにした。
さて、量子通信も一部の国では実用化され、非局所性(量子力学Ver.2)が静かなブームにある。
ところで、量子力学Ver.1の波動関数の波束への収縮を光子について理解しておくと、もつれた2光子が互いに反対方向に飛んで行った半径1光年の先で片方の光子が観測された場合(波束に収縮した場合)、その情報が2光年彼方のもう一方の光子に瞬時に伝わると考えると非局所性をイメージしやすい。
[1]波動関数の波束への収縮 量子力学Ver.1
が
- 光の三次元波動方程式のグリーン関数を用いて、ベクトルポテンシャルの満たす波動方程式を解く。
- 源泉(光源の電流分布)が三次元波動方程式のグリーン関数(球面波)で伝播し、伝播後の波を時間微分したもの(電場:E)がもう一度電流分布と相互作用しているという描像に到達。
- 観測⇔光源から出た光が360度の全方向に放射された光のごく一部(ごく小さな立体角)を見る⇔観測装置と光源との方向が決まるとして、電場E(平面波)の波数ベクトルkを観測によって決まったk0でテーラー展開。
- 包絡線がデルタ関数で群速度がcの波束を得た。
- すなわち、球面波の時間微分で表される電場(平面波)が、観測することによって包絡線がデルタ関数の波束に収縮した。
としている。物質波もこのようにして考えることができる。シュレーディンガー方程式は
iħ(∂/∂r)Ψa(k) = ħωΨa(k)
だが、電子の場合は添え字a (a = 1, 2) がスピンを、光子の場合が偏光を表す。
[2]非局所性 量子力学Ver.2
「もつれた2光子が互いに反対方向に飛んで行った半径1光年の先で片方の光子が観測された場合(波束に収縮した場合)、その情報が2光年彼方のもう一方の光子に瞬時に伝わる。」と言うのは時間的に外挿していることを除けば単なる事実に過ぎない。
そのメカニズムは未だ解明されていないが、相互作用(行列)の閉じたネットワーク(開いていると統計力学が示すようにエントロピーに支配されてしまう:参照)が有り、これが時間にも距離にも依存しないと考えられている。
ハドロンの周期表みたいなものをシミュレートすることで検証されてはいるものの、可能なネットワークの種類が多すぎて一つに絞り切れていない状況である。
こういうときはとりあえず原理として片づけておく。
原理とは、それ以上ブレークダウンできないもの。
[3]重ね合わせ 量子力学Ver.1
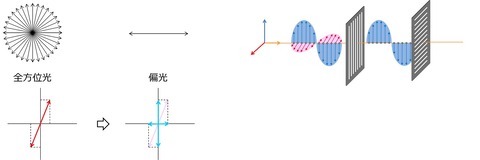
これも「光しばり(リャンハンしばり、みたいな感じで)」で説明するには偏光が良いと思って、を挙げておいたのだが...
これがぴんとこなかったのかもしれない。
そこで別の説明を考えてみた。
光波であれ物質波であれ、その状態関数(波動関数)は複素関数で表現される。物理量は状態関数の複素共役との積で表される(間に何も挟まなければ存在確率となるし、何か挟めば挟んだものに対応する物理量になる。)。
複素数は例えばz(+) = x + iy (x, y ∈ R) で表現されるが、複素共役との積はz(+)z(-) = x^2 - y^2だから必ず実数になる。すなわち、複素数で表されるものの物理量は少なくとも二つの状態:z(+)とz(-)の重ね合わせなのである。
iħ(∂/∂r)Ψa(k) = ħωΨa(k)
だが、電子の場合は添え字a (a = 1, 2) がスピンを、光子の場合が偏光を表す。
[2]非局所性 量子力学Ver.2
「もつれた2光子が互いに反対方向に飛んで行った半径1光年の先で片方の光子が観測された場合(波束に収縮した場合)、その情報が2光年彼方のもう一方の光子に瞬時に伝わる。」と言うのは時間的に外挿していることを除けば単なる事実に過ぎない。
そのメカニズムは未だ解明されていないが、相互作用(行列)の閉じたネットワーク(開いていると統計力学が示すようにエントロピーに支配されてしまう:参照)が有り、これが時間にも距離にも依存しないと考えられている。
ハドロンの周期表みたいなものをシミュレートすることで検証されてはいるものの、可能なネットワークの種類が多すぎて一つに絞り切れていない状況である。
こういうときはとりあえず原理として片づけておく。
原理とは、それ以上ブレークダウンできないもの。
[3]重ね合わせ 量子力学Ver.1
これも「光しばり(リャンハンしばり、みたいな感じで)」で説明するには偏光が良いと思って、を挙げておいたのだが...
これがぴんとこなかったのかもしれない。
そこで別の説明を考えてみた。
光波であれ物質波であれ、その状態関数(波動関数)は複素関数で表現される。物理量は状態関数の複素共役との積で表される(間に何も挟まなければ存在確率となるし、何か挟めば挟んだものに対応する物理量になる。)。
複素数は例えばz(+) = x + iy (x, y ∈ R) で表現されるが、複素共役との積はz(+)z(-) = x^2 - y^2だから必ず実数になる。すなわち、複素数で表されるものの物理量は少なくとも二つの状態:z(+)とz(-)の重ね合わせなのである。